Biologia - Matura Czerwiec 2017, Poziom rozszerzony (Formuła 2015) - Zadanie 2.
Informacja genetyczna warunkująca oporność drobnoustrojów na leki może być zapisana
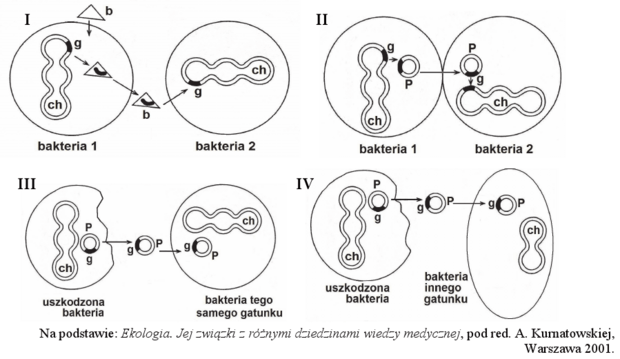
w ich chromosomach lub plazmidach. Na rysunkach I–IV przedstawiono cztery różne
sposoby nabywania lekooporności przez bakterie, które należą do tego samego gatunku (I–III)
lub należące do różnych gatunków (IV).
Zastosowane oznaczenia: g – gen lekooporności, b – bakteriofag, ch – chromosom bakteryjny,
P – plazmid.
2.1. (0–1)
Podaj oznaczenie rysunku: I, II, III lub IV, na którym przedstawiono koniugację bakterii i określ, dlaczego koniugacja nie jest sposobem rozmnażania.
2.2. (0–1)
Na podstawie schematu oceń, czy poniższe stwierdzenia dotyczące sposobów nabywania lekooporności przez bakterie są prawdziwe. Zaznacz P, jeśli stwierdzenie jest prawdziwe, albo F – jeśli stwierdzenie jest fałszywe.
| 1. | Koniugacja u bakterii może się przyczynić do przenoszenia genu lekooporności wyłącznie pomiędzy różnymi gatunkami bakterii. | P | F |
| 2. | Bakterie mogą stać się lekooporne, jeżeli nabędą odpowiedni gen lub plazmid z genem tylko od innych, żywych bakterii. | P | F |
| 3. | Wirusy atakujące komórki bakterii mogą się przyczynić do przenoszenia genu lekooporności między nimi. | P | F |
Rozwiązanie
2.1. (0–1)
Schemat punktowania
1 p. – za prawidłowy wybór procesu II oraz właściwe wyjaśnienie uwzględniające brak
zwiększenia się liczby komórek potomnych.
0 p. – za każdą inną odpowiedź lub za brak odpowiedzi.
Przykładowe rozwiązania
- II – nie jest sposobem rozmnażania, ponieważ w wyniku tego procesu nie zwiększa się liczba komórek potomnych.
- II – ponieważ jest to zjawisko wymiany części materiału genetycznego między uczestniczącymi komórkami, w wyniku czego nie zmienia się liczba komórek.
2.2. (0–1)
Schemat punktowania
1 p. – za poprawną ocenę trzech stwierdzeń dotyczących sposobów nabywania lekooporności
przez bakterie.
0 p. – za każdą inną odpowiedź lub za brak odpowiedzi.
Rozwiązanie
1 – F, 2 – F, 3 – P
