Chemia - Zbiór zadań problemowych CKE, Poziom rozszerzony (Formuła 2023)
Zadanie 1. (4 pkt)
O atomie pierwiastka X wiadomo, że:
- 20 spośród wszystkich elektronów w atomie opisanych jest liczbą kwantową 𝑙 = 2
- elektrony walencyjne atomu X w stanie podstawowym opisane są dwiema różnymi wartościami pobocznej liczby kwantowej (𝑙 = 0 i 𝑙 = 1), przy czym liczba elektronów walencyjnych opisanych poboczną liczbą kwantową 𝑙 = 1 jest większa, niż liczba elektronów walencyjnych opisanych poboczną liczbą kwantową 𝑙 = 0
- tylko jeden z elektronów walencyjnych jest niesparowany.
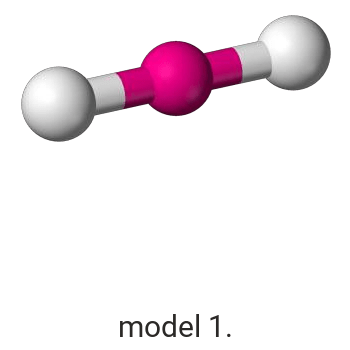
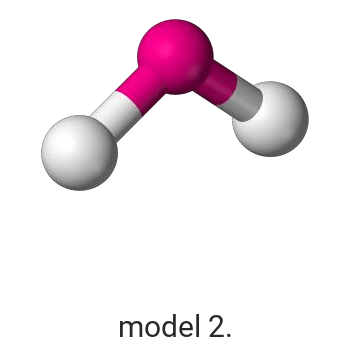
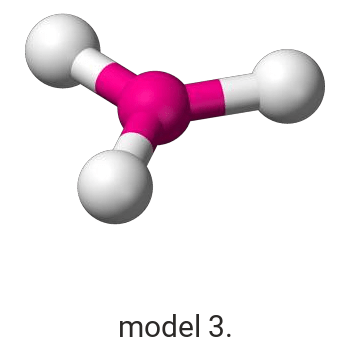
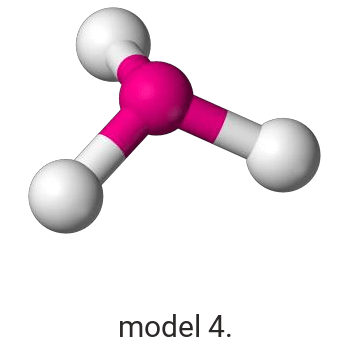
Pierwiastek X reaguje z chlorem, w wyniku czego powstaje związek, w którym procentowa masowa zawartość chloru wynosi 45,6%.
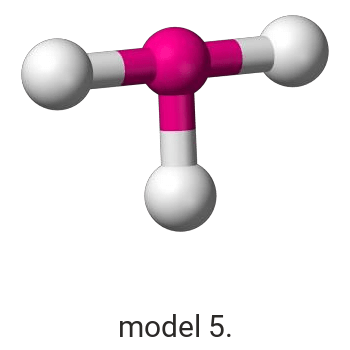
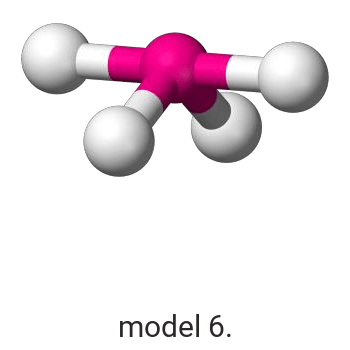
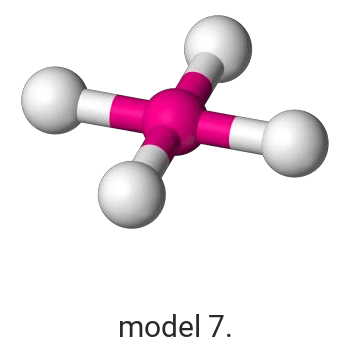
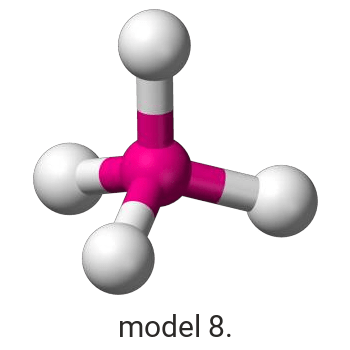
Wykonaj odpowiednie obliczenia i wskaż model, który przedstawia budowę przestrzenną cząsteczki związku pierwiastka X z chlorem.
Model:
Zadanie 2. (4 pkt)
Rentgenografia strukturalna jest jedyną techniką badawczą, która pozwala, z niemal absolutną pewnością, określać struktury przestrzenne związków chemicznych (np. dokładną strukturę skomplikowanych cząsteczek związków organicznych). Ta technika polega na naświetlaniu kryształu badanego związku promieniami rentgenowskimi. Uzyskany obraz, nazywany obrazem dyfrakcyjnym, poddaje się zaawansowanej obróbce matematycznej, dzięki czemu można wygenerować mapę rozkładu gęstości chmury elektronowej w cząsteczce, która mówi o wzajemnym ułożeniu w przestrzeni atomów tworzących cząsteczkę. Do uzyskanego obrazu można następnie dopasować najbardziej prawdopodobny model cząsteczki.
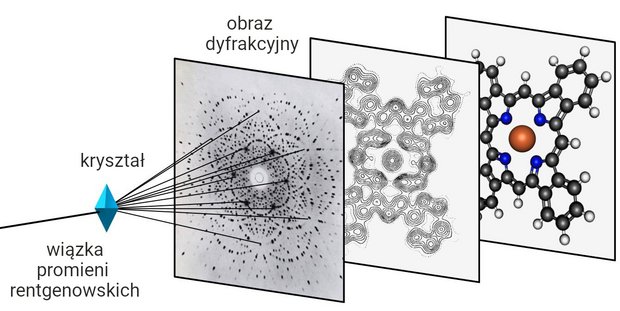
Poniżej przedstawiono mapę gęstości elektronowej uzyskaną metodą rentgenografii strukturalnej dla pewnej halogenopochodnej fenolu zawierającej masowo 15,3% węgla.
Wykonaj odpowiednie obliczenia i narysuj wzór strukturalny cząsteczki badanego związku oraz podaj jego nazwę systematyczną.
Nazwa systematyczna:
Zadanie 3. (4 pkt)
W trakcie mieszania dwóch cieczy sumaryczna masa roztworu jest równa sumie mas mieszanych składników, jednak końcowa objętość mieszaniny jest najczęściej różna od sumy objętości mieszanych składników. Zjawisko zmniejszenia lub zwiększenia objętości cieczy podczas mieszania nazywamy odpowiednio kontrakcją lub dylatacją objętości.
W tabeli poniżej przedstawiono wartości gęstości wodnego roztworu kwasu siarkowego(VI) w zależności od jego stężenia w temperaturze 20°C.
| Procent masowy H2SO4 | Gęstość, g∙cm–3 |
|---|---|
| 1 | 1,005 |
| 5 | 1,032 |
| 10 | 1,066 |
| 20 | 1,139 |
| 30 | 1,219 |
| 40 | 1,303 |
| 45 | 1,348 |
| 50 | 1,395 |
| 55 | 1,445 |
| 60 | 1,498 |
| 65 | 1,553 |
| 70 | 1,611 |
| 80 | 1,727 |
| 90 | 1,814 |
| 93 | 1,828 |
| 96 | 1,836 |
| 100 | 1,831 |
Gęstość wody w temperaturze 20°C wynosi 0,998 g ∙ cm–3
Wykonaj odpowiednie obliczenia i na ich podstawie uzupełnij poniższy tekst.
- Rozcieńczanie kwasu siarkowego(VI) to proces egzotermiczny. W wyniku zmieszania równych objętości wody i stężonego roztworu kwasu siarkowego(VI) o stężeniu 93% masowych i ochłodzeniu otrzymanego roztworu do temperatury 20°C, sumaryczna objętość cieczy (maleje / rośnie) o wartość równą % w porównaniu do sumy objętości cieczy przed zmieszaniem.
- Spowodowane jest to (różną / taką samą) wielkością cząsteczek wody i kwasu siarkowego(VI) oraz (większą / mniejszą / taką samą) energią oddziaływań między drobinami obecnymi w wodnym roztworze kwasu siarkowego(VI) w porównaniu do siły oddziaływań cząsteczek H2O ⋯ H2O i H2SO4 ⋯ H2SO4.
Zadanie 4. (4 pkt)
Wpływ temperatury na szybkość reakcji tłumaczy się wykładniczym wzrostem wartości stałej szybkości reakcji 𝑘. Tę zależność opisuje równanie Arrheniusa:
𝑘 = 𝐴 ∙ e–𝐸a𝑅∙𝑇
gdzie 𝐸a oznacza energię aktywacji, 𝑅 – uniwersalną stałą gazową, a 𝑇 – temperaturę bezwzględną wyrażoną w kelwinach. Czynnik e–𝐸a𝑅∙𝑇 informuje o tym, jaka część zderzających się molekuł ma energię większą lub równą energii aktywacji, natomiast czynnik 𝐴, nazywany czynnikiem przedwykładniczym, określa częstotliwości zderzeń efektywnych. Wartość czynnika 𝐴 jest w praktyce niezależna od temperatury. Równanie Arrheniusa może być przekształcone do postaci logarytmicznej:
ln(𝑘) = – 𝐸a𝑅 ∙ 1𝑇 + ln𝐴
będącej równaniem liniowym (𝑦=𝑎𝑥+𝑏), opisującym zależność logarytmu naturalnego1 ze stałej szybkości reakcji ln(𝑘) od odwrotności temperatury 1𝑇. Wartość (– 𝐸a𝑅) jest współczynnikiem kierunkowym tej prostej.
Badano przebieg reakcji chemicznej, zachodzącej między wodorem i chlorkiem bromu, przebiegającej według następującego równania reakcji:
H2 (g) + 2BrCl (g) → Br2 (g) + 2HCl (g)
Po ustaleniu mechanizmu opisanej reakcji określono jej równanie kinetyczne jako:
𝑣 = 𝑘 ∙ 𝑐H2 ∙ 𝑐BrCl
Tę reakcję przeprowadzano w różnych temperaturach należących do przedziału od 310 K do 380 K i za każdym razem wyznaczono wartość jej stałej szybkości. Otrzymane dane zestawiono w tabeli.
| Nr pomiaru | Temperatura 𝑇, K | Stała szybkości reakcji 𝑘, dm3 ∙ mol−1 ∙ s−1 |
|---|---|---|
| 1 | 310 | 5,33∙10–3 |
| 2 | 320 | 6,90∙10–3 |
| 3 | 330 | 8,78∙10–3 |
| 4 | 340 | 11,02∙10–3 |
| 5 | 350 | 13,66∙10–3 |
| 6 | 360 | 16,73∙10–3 |
| 7 | 370 | 20,26∙10–3 |
| 8 | 380 | 24,29∙10–3 |
1 logarytm o podstawie równej liczbie Eulera, wynoszącej e ≈ 2,7183, podlega takim samym regułom działań jak pozostałe logarytmy o innych podstawach należących do zbioru liczb rzeczywistych.
Uzupełnij tabelę brakującymi wartościami ln(𝒌) (z dokładnością do dwóch miejsc po przecinku) oraz narysuj wykres zależności logarytmu naturalnego ze stałej szybkości reakcji pomiędzy wodorem a chlorkiem bromu ln(𝒌) od odwrotności temperatury 1𝑇. Następnie oblicz wartość energii aktywacji tej reakcji.
Obliczenia pomocnicze do narysowania wykresu:
| 1𝑇 ∙ 105, K–1 | 323 | 313 | ||||||
| ln(𝑘) | –5,23 | –4,98 |
Wykres:
Obliczenia:
Zadanie 5. (4 pkt)
W zamkniętym reaktorze w stałej objętości (V = 1,00 dm3) znajduje się początkowa ilość gazowego substratu A równa 𝑛oA =1,100 mol. Układ ogrzano do temperatury 550°C, co zapoczątkowało reakcję rozkładu substratu A do gazowego produktu B. Układ termostatowano przez pewien czas, do ustalenia się równowagi dynamicznej pomiędzy reagentami A i B.
Na wykresie przedstawiono wyniki pomiaru stężeń reagentów A i B w trakcie trwania reakcji do momentu ustalenia się stanu równowagi dynamicznej w podanej temperaturze.
Po trzydziestu minutach od momentu osiągnięcia stanu równowagi od początku eksperymentu, po osiągnięciu stanu równowagi, do reaktora wprowadzono dodatkowo 0,800 mol reagenta A.
Uwagi od BiologHelp:
Zmodyfikowano oryginalną treść zadania od CKE, aby pokrywała się ona z poniższym wykresem załączonym do zadania oraz treścią polecenia.
Uzupełnij wykres tak, aby przedstawiał zmiany stężeń reagentów A i B w czasie trwania reakcji, od momentu wprowadzenia do układu dodatkowej ilości reagenta A (𝒕 = 𝟑𝟎 𝐦𝐢𝐧) do momentu zakończenia eksperymentu (𝒕 = 𝟔𝟎 𝐦𝐢𝐧).
Obliczenia:
Zadanie 6. (4 pkt)
Cząsteczki kwasu etanowego mogą łączyć się wiązaniami wodorowymi i tworzyć dimer:
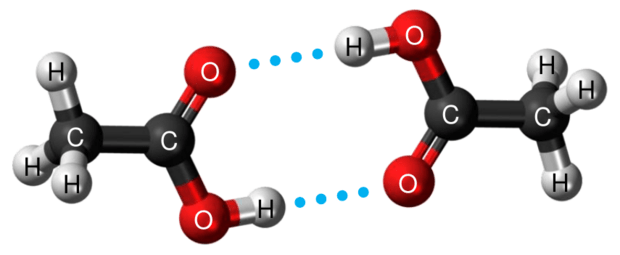
Ten dimer występuje w stanie gazowym oraz w roztworach kwasu etanowego w rozpuszczalnikach nietworzących z nim wiązań wodorowych.
Roztwór 60,0 g kwasu octowego (1,00 mol) w 100,0 g benzenu wykazuje temperaturę wrzenia wyższą o 20,1°C względem wrzenia czystego benzenu. Podwyższenie temperatury wrzenia rozpuszczalnika jest proporcjonalne do łącznej liczby drobin substancji rozpuszczonej w rozpuszczalniku. Tę zależność opisuje poniższy wzór:
Δ𝑡 = 𝐾b ∙ 𝑛𝑚r
gdzie Δ𝑡 to różnica temperatury wrzenia roztworu i czystego rozpuszczalnika (wyrażona w °C), 𝑛 – sumaryczna liczba drobin w roztworze (wyrażona w molach), 𝑚r – masa rozpuszczalnika (wyrażona w kilogramach), a 𝐾b – stała ebulioskopowa, której wartość dla benzenu wynosi 2,51°C ∙ kg ∙ mol–1.
Oblicz stężeniową stałą równowagi reakcji:
2CH3COOH ⇄ (CH3COOH)2
w temperaturze T. W obliczeniach pomiń autodysocjację kwasu octowego i przyjmij, że otrzymany roztwór CH3COOH w benzenie miał gęstość równą 0,96 g ∙ cm–3.
Zadanie 7. (4 pkt)
W roztworze zawierającym jony Cu2+ oraz jony Cl– ustala się równowaga przedstawiona poniższym równaniem:
Cu2+ (aq) + 4Cl– (aq) ⇄ CuCl2–4 (aq) Δ𝐻>0
Przygotowano roztwór zawierający jony Cl– (aq), Cu2+ (aq) i CuCl2–4 (aq), przy czym stężenia dwóch ostatnich były sobie równe. Temperatura roztworu wynosiła 25°C. Następnie roztwór ogrzano do temperatury 80°C. Na zdjęciach obok przedstawiono wygląd roztworu w temperaturze 25°C i w temperaturze 80°C.

Uzupełnij poniższą Tabelę 1. Następnie w Tabeli 2. wpisz numer zdjęcia przedstawiającego wygląd probówki z roztworem jonów Cu2+ i CuCl2–4 o temperaturze 25°C po dodaniu kilku cm3 cieczy wymienionych w tej tabeli.
Tabela 1.
| Nazwa jonu biorącego udział w przedstawionej równowadze | |||
| Barwa roztworu jonów |
Tabela 2.
| Ciecz dodana do probówki zawierającej opisany układ równowagowy w 𝑡= 25°C | Stężony kwas solny | Woda | Stężony wodny roztwór azotanu(V) srebra(I) |
| Numer zdjęcia |
Zadanie 8. (4 pkt)
Cynk jest metalem, który ulega reakcji zarówno z kwasami słabo utleniającymi, jak i silnie utleniającymi. W reakcjach z roztworami kwasu azotowego(V) cynk się utlenia, w wyniku czego tworzą się sole, w których występuje on na II stopniu utlenienia, natomiast – formalnie – atomy azotu z kwasu azotowego obniżają swój stopień utlenienia zależnie od stężenia użytego kwasu. Zależność stopnia utlenienia atomu azotu w dominującym produkcie gazowym reakcji cynku z kwasem azotowym(V) oraz dodatkowe informacje dotyczące powstającego produktu przedstawiono w poniższej tabeli.
| Stężenie kwasu azotowego(V) 𝑐HNO3, % | Stopień utlenienia atomu azotu w produkcie gazowym | Dodatkowe informacje o produkcie gazowym |
|---|---|---|
| < 3% | produkt gazowy nie zawiera atomu azotu | bezbarwny, palny |
| 3% – 9% | – | brak produktu gazowego |
| 10% – 19% | 0 | bezbarwny, niepalny |
| 20% – 29% | +I | bezbarwny |
| 30% – 59% | +II | bezbarwny, brązowieje w kontakcie z powietrzem |
| > 60% | +IV | brunatny |
Przeprowadzono następujące doświadczenie: do kolby miarowej o pojemności 500,00 cm3 wprowadzono 175,00 cm3 kwasu azotowego(V) o stężeniu 11,90 mol ∙ dm–3, a następnie kolbę dopełniono wodą destylowaną do kreski, w wyniku czego otrzymano roztwór o gęstości 1,05 g ∙ cm–3. Następnie do zlewki wprowadzono 400,00 cm3 otrzymanego roztworu i wrzucono ostrożnie granulki cynku.
Napisz w formie jonowej, z uwzględnieniem liczby oddawanych lub pobieranych elektronów (zapis jonowo-elektronowy), równania reakcji redukcji i utleniania zachodzących podczas opisanego procesu roztwarzania cynku w przygotowanym roztworze kwasu azotowego(V) oraz sumaryczne równanie tej reakcji (w formie cząsteczkowej) prowadzącej do otrzymania produktu dominującego.
Równanie reakcji utleniania:
Równanie reakcji redukcji:
Sumaryczne równanie reakcji w formie cząsteczkowej:
Zadanie 9. (4 pkt)
Cer może tworzyć związki chemiczne wyłącznie na +III (bezbarwne sole) albo na +IV stopniu utlenienia (związki czerwono-pomarańczowe). Roztwory soli ceru(IV) można stosować do miareczkowania wszystkich substancji organicznych i nieorganicznych o właściwościach redukujących. Roztwory zawierające kation Ce4+ otrzymuje się poprzez rozpuszczenie w wodzie lub rozcieńczonym kwasie siarkowym(VI) dwuwodnego siarczanu(VI) amonu ceru(IV) (NH4)4Ce(SO4)4 ∙ 2H2O, który dysocjuje całkowicie na jony amonowe, ceru(IV) i siarczanowe(VI). Substancją zalecaną do ustalenia dokładnej wartości stężenia molowego kationów Ce4+ (nastawienia miana roztworu) jest tlenek arsenu(III) As2O3. Reakcja pomiędzy jonami ceru(IV) a tlenkiem arsenu(III) prowadzi do powstania kwasu arsenowego(V) H3AsO4 i odbarwienia roztworu.
W celu ustalenia stężenia molowego pewnej substancji organicznej przygotowano roztwór mianowany jonów ceru Ce4+ poprzez rozpuszczenie 𝑚𝑥 gramów dwuwodnego siarczanu(VI) amonu ceru(IV) w wodzie destylowanej i dopełnienie roztworu wodą do całkowitej objętości równej 1,000 dm3 (czyli 1 dm3 podany z dokładnością do 3 miejsc po przecinku, inaczej 1000 cm3 − przypis od BiologHelp). Podczas nastawiania miana roztworu jonów ceru Ce4+, 200,0 cm3 tego roztworu przereagowało dokładnie z 1,790 g tlenku arsenu(III).
Oblicz, ile gramów dwuwodnego siarczanu(VI) amonu ceru(IV) zużyto do przygotowania roztworu mianowanego kationów ceru(IV).
Uwagi od BiologHelp:
Przypis do treści zadania dodany ze względu na zgłoszenia związane z błędną interpretacją zapisu 1,000 dm3 jako 1000 dm3.
Zadanie 10. (4 pkt)
Większość soli potasu jest dobrze lub bardzo dobrze rozpuszczalna w wodzie. Jedną z nielicznych soli potasu słabo rozpuszczalnych w wodzie jest chloran(VII) potasu. Iloczyn rozpuszczalności tej soli, w temperaturze 20°C, wynosi 𝐾S(KClO4) = 1,05 · 10–2. Z tego powodu aniony chloranowe(VII) są odczynnikiem stosowanym w jakościowej analizie chemicznej do wykrywania obecności kationów potasu. Pojawienie się białego osadu, po dodaniu do badanego roztworu kilku cm3 nasyconego roztworu chloranu(VII) sodu, świadczy o obecności kationów potasu w tym roztworze:
K++ ClO–4 ⟶ KClO4↓
Rozpuszczalności chloranu(VII) sodu w wodzie, w temperaturze 20°C, wynosi
𝑅NaClO4 = 205,0 g100 g H2O,
a gęstość nasyconego roztworu tej soli w temperaturze 20°C wynosi
𝑑r.nas.NaClO4 = 1,58 g∙cm–3.
Rozstrzygnij, czy dodanie 2,00 cm3 nasyconego (w temperaturze 20°C) roztworu chloranu(VII) sodu do 15,00 cm3 roztworu chlorku potasu o stężeniu molowym równym 0,020 mol ∙ dm–3 spowoduje, że wytrąci się osad chloranu(VII) potasu. Załóż, że objętość otrzymanej mieszaniny jest sumą objętości roztworów przed zmieszaniem. Odpowiedź uzasadnij odpowiednimi obliczeniami.
Zadanie 11. (4 pkt)
Wskaźniki kwasowo-zasadowe są słabymi kwasami lub słabymi zasadami. Przykładowy wskaźnik o wzorze ogólnym HIn ulega dysocjacji kwasowej i w roztworze wodnym ustala się równowaga:
HIn (aq) + H2O ⇄ H3O+ (aq) + In– (aq)
Obie formy wskaźnika stanowiące sprzężoną parę kwas–zasada Brønsteda: kwasowa – HIn (aq) i zasadowa – In–(aq), nadają roztworom wskaźnika dwie wyraźnie różne barwy. Załóżmy, że forma cząsteczkowa HIn (aq) zabarwia roztwór wodny wskaźnika na kolor różowy, a forma jonowa In–(aq) – na kolor błękitny. Jeśli do roztworu wskaźnika HIn wprowadzimy kwas lub zasadę, to położenie stanu równowagi – zgodnie z regułą przekory Le Chateliera–Brauna – ulegnie zmianie, co poskutkuje zmianą barwy mieszaniny.
W roztworze kwasowym obserwujemy kolor różowy wywołany obecnością drobin HIn, a w roztworze zasadowym – wskutek obecności jonów In– – kolor błękitny. Jeżeli stężenia obu form są porównywalne, wskaźnik przyjmuje kolor pośredni.
Wyrażenie na stałą dysocjacji jonowej wskaźnika jako słabego kwasu ma postać:
𝐾in = [H3O+(aq)] [In-(aq)][HIn (aq)]
Gdy stężenia form In–(aq) i HIn (aq) będą równe, to:
𝐾in = [H+(aq)] [In-(aq)][HIn (aq)] = [H+(aq)]
Obliczenie ujemnego logarytmu dziesiętnego z obu stron równania prowadzi do wyrażenia:
pKin = pH
Wartość pKin ±1 umownie przyjmuje się jako zakres działania wskaźnika kwasowo-zasadowego. Jeżeli do kolby zawierającej analit (roztwór kwasu o nieznanym stężeniu) dodajemy kroplami, z biurety, roztwór titranta (roztwór o odczynie zasadowym, którego stężenie ma znaną wartość), to mówimy o miareczkowaniu kwasowo-zasadowym. Pomiar pH roztworu analitu w funkcji objętości dodawanego titranta pozwala sporządzić krzywą miareczkowania. Na krzywej wyróżnia się fragment niemalże prostopadły do osi zmiennej niezależnej, który pozwala na odczytanie tzw. punktu równoważnikowego, czyli wartości pH, dla której do roztworu wprowadzono tę samą liczbę moli zarówno kwasu, jak i zasady. W przypadku wskaźnika poprawnie dobranego do takiego miareczkowania oczekuje się, że w zakresie działania tego wskaźnika mieści się punkt równoważnikowy.
Do kolby zawierającej 25,00 cm3 kwasu solnego o stężeniu 0,010 mol ∙ dm–3 wprowadzano kroplami, z biurety napełnionej do objętości 50,0 cm3, wodny roztwór amoniaku o stężeniu 0,020 mol ∙ dm–3. Przygotowano zestaw wskaźników kwasowo-zasadowych wraz z dotyczącymi ich dodatkowymi informacjami zestawionymi w tabeli:
| Nazwa wskaźnika | błękit tymolowy | oranż metylowy | purpura bromokrezolowa | błękit bromotymolowy | czerwień fenolowa | fenoloftaleina |
| p𝐾in | 1,7 | 3,4 | 5,8 | 7,0 | 7,9 | 9,4 |
Podaj nazwę wskaźnika, który powinien zostać użyty do wyznaczenia punktu końcowego podczas opisanego miareczkowania kwasowo-zasadowego. Załóż, że końcowa objętość roztworu (w punkcie końcowym miareczkowania) jest równa sumie objętości analitu i titranta.
Zadanie 12. (4 pkt)
Zalkalizowana zawiesina świeżo wytrąconego wodorotlenku miedzi(II) jest ważnym odczynnikiem stosowanym w organicznej analizie chemicznej. Wodorotlenek miedzi(II) reaguje z rozmaitymi związkami organicznymi, w wyniku czego daje różne objawy reakcji. Te efekty mogą być różne w zależności od tego, czy reakcję przeprowadzono w temperaturze pokojowej, czy – po podgrzaniu. Poniżej przedstawiono zdjęcia zawartości probówek po reakcji wodorotlenku miedzi(II), zalkalizowanego roztworem wodorotlenku sodu, ze związkami należącymi do różnych grup związków organicznych, zarówno w temperaturze pokojowej, jak i po podgrzaniu.
O cząsteczce pewnego związku organicznego X wiadomo, że:
- jest chiralna
- ma budowę łańcuchową
- jej masa cząsteczkowa nie przekracza 100 u
- atomy węgla stanowią 40,0 % masy tej cząsteczki
- atomy tlenu stanowią 53,3 % masy tej cząsteczki
- orbitalom walencyjnym tylko jednego atomu węgla można przypisać hybrydyzację typu sp2
- każdy atom węgla jest połączony z jednym atomem tlenu.
Wodny roztwór związku X poddano próbie ze świeżo strąconą, zalkalizowaną wodorotlenkiem sodu, zawiesiną wodorotlenku miedzi(II). Doświadczenia przeprowadzono w temperaturze pokojowej (𝑡 = 25°C) oraz w podwyższonej temperaturze (𝑡 = 90°C).
Wskaż, jakie będą objawy opisanych doświadczeń – wybierz odpowiedni numer zdjęcia (spośród przedstawionych powyżej). Zapisz równania reakcji przebiegających podczas obu doświadczeń lub zaznacz, że żadna reakcja wtedy nie zachodzi. Uzupełnij poniższą tabelę. Zastosuj wzory półstrukturalne (grupowe) lub uproszczone (szkieletowe) związków organicznych, nie uwzględniaj stereoizomerii.